一造《案例分析》決策樹考點曾在2016年及2019年造價考試中出過題,而近幾年來都沒出現過,2023年出題的概率比較大,要求能夠繪制決策樹并計算與決策。
結合老師視頻講解,思路更清晰↓↓↓
決策樹是以方框和圓圈為節點,并由直線連接而成的一種像樹枝形狀的結構,其中,方框表示決策點,圓圈表示機會點;從決策點畫出的每條直線代表一個方案,叫作方案枝,從機會點畫出的每條直線代表一種自然狀態,叫作概率枝。(如下圖所示)
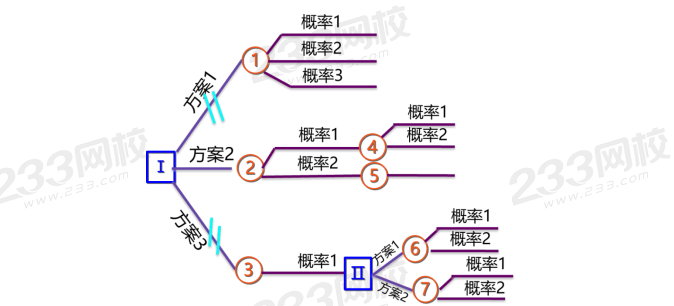
用決策點代表決策問題,方案枝代表可選方案,機會點(狀態點)代表備選方案的經濟效果,概率枝代表方案可能出現的各種概率,概率枝后面的數值代表不同方案在不同狀態下可獲得的損益值(又可包括機會點、決策點)。通過對各方案的期望值進行計算比較,為決策者提供決策依據。
繪圖步驟及計算
1、決策樹的繪制是自左向右(決策點和機會點的編號左小右大,上小下大),而計算則是自右向左。
2、各機會點的期望值計算結果應標在該機會點上方;
3、最后將決策方案以外的方案枝用兩短線排除。
A企業結合自身情況和投標經驗,認為該工程項目投高價標的中標概率為40%,投低價標的中標概率為60%。投高價標中標后,收益效果好、中、差三種可能性的概率分別為30%、60%、10%,計入投標費用后的凈損益值分別為40萬元、35萬元、30萬元;投低價標中標后,收益效果好、中、差三種可能性的概率分別為15%,60%,25%,計入投標費用后的凈損益值分別為30萬元、25萬元、20萬元;投標相關費用為5萬元,A企業經測算、評估后,最終選擇了投低價標,投標價為500萬元。

機會點③期望值:0.3×40+0.6×35+0.1×30=36.00萬
機會點④期望值:0.15×30+0.6×25+0.25×20=24.50萬
機會點①期望值:36×0.4-0.6×5=11.40萬
機會點②期望值:24.5×0.6-0.4×5=12.70萬
機會點②的期望值大于①,故應選擇投低標
如果你喜歡這篇文章,可以點擊側邊【收藏★】下來哦~
溫馨提示:文章由作者233網校-ljt獨立創作完成,未經著作權人同意禁止轉載。


