一、資產組合的風險與收益
(一)資產組合含義
兩個或兩個以上資產所構成的集合，稱為資產組合。如果資產組合中的資產均為有價證券，則該資產組合也可稱為證券組合。
(二)資產組合的預期收益率 [E(Rp)]來源：考試大
資產組合的預期收益率，就是組成資產組合的各種資產的預期收益率的加權平均數，其權數等于各種資產在整個組合中所占的價值比例。即：
E(Rp)=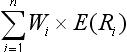
式中 式中，E(Ri)表示第i種資產的預期收益率;
Wi表示第i種資產在整個組合中所占的價值比值。 設為首頁
(三)資產組合風險的度量
1.兩項資產組合的風險
兩項資產組合的收益率的方差滿足以下關系式：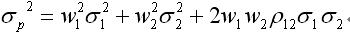
式中：
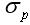表示資產組合的標準差，衡量資產組合的風險;
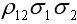表示兩項資產的協方差
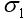和
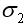分別表示組合中兩項資產的標準差;
w1和w2分別表示組合中兩項資產所占的價值比例;
反映兩項資產收益率的相關程度，即兩項資產收益率之間相對運動的狀態，稱為相關系數。理論上，相關系數處于區間 [-1，1]內。
① 當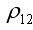
=1時，表明兩項資產的收益率具有完全正相關的關系，即它們的收益率變化方向和變化幅度完全相同，這時，
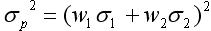，即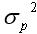
達到最大。由此表明，組合的風險等于組合中各項資產風險的加權平均值。換句話說， 當兩項資產的收益率完全正相關時，兩項資產的風險完全不能互相抵消，所以這樣的資產組合不能降低任何風險。
②當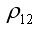 
=1時，表明兩項資產的收益率具有完全負相關的關系，即它們的收益率變化方向和變化幅度完全相反。這時，
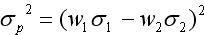，即 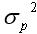達到最小，甚至可能是零。因此，當兩項資產的收益率具有完全負相關關系時，兩者之間的風險可以充分地相互抵消，甚至完全消除。因而， 由這樣的資產組成的組合就可以最大程度地抵消風險。
③在實際中，兩項資產的收益率具有完全正相關或完全負相關關系的情況幾乎是不可能的。絕大多數資產兩兩之間都具有不完全的相關關系，即相關系數小于1且大于-1(多數情況下大于零)因此，會有0<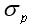 
< 
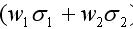，即資產組合的標準差小于組合中各資產標準差的加權平均，也即資產組合的風險小于組合中各資產風險之加權平均值，因此資產組合才可以分散風險。
2.多項資產組合的風險
一般來講，由于每兩項資產間具有不完全的相關關系，因此隨著資產組合中資產個數的增加，資產組合的風險會逐漸降低。但當資產的個數增加到一定程度時，資產組合的風險程度將趨于平穩，這時資產組合風險的降低將非常緩慢直至不再降低。
那些只反映資產本身特性，由方差表示的各資產本身的風險，會隨著組合中資產個數的增加而逐漸減小，當組合中資產的個數足夠大時，這部分風險可以被完全消除。我們將這些可通過增加組合中資產的數目而最終消除的風險稱為非系統風險。
而那些由協方差表示的各資產收益率之間相互作用、共同運動所產生的風險，并不能隨著組合中資產數目的增加而消失，它是始終存在的。這些無法最終消除的風險被稱為系統風險。
二、非系統風險與風險分散
非系統風險，又被稱為企業特有風險或可分散風險，是指由于某種特定原因對某特定資產收益率造成影響的可能性。它是可以通過有效的資產組合來消除掉的風險;它是特定企業或特定行業所特有的，與政治、經濟和其他影響所有資產的市場因素無關。對于特定企業而言，企業特有風險可進一步分為經營風險和財務風險。
1、經營風險，是指因生產經營方面的原因給企業目標帶來不利影響的可能性。
2、財務風險，又稱籌資風險，是指由于舉債而給企業目標帶來不利影響的可能性。
在風險分散的過程中，不應當過分夸大資產多樣性和資產數目的作用。實際上，在資產組合中資產數目較少時，通過增加資產的數目，分散風險的效應會比較明顯，但當資產的數目增加到一定程度時，風險分散的效應就會逐漸減弱。
04年單選.在證券投資中，通過隨機選擇足夠數量的證券進行組合可以分散掉的風險是( )
A. 所有風險 B. 市場風險
C. 系統性風險 D. 非系統性風險
答案：D
07年判斷.證券組合風險的大小，等于組合中各個證券風險的加權平均數。( )
答案：×
解析：只有在證券之間的相關系數為1時，組合的風險才等于組合中各個證券風險的加權平均數;如果相關系數小于1，那么證券組合的風險就小于組合中各個證券風險的加權平均數。
三、系統風險及其衡量
系統風險，又被稱為市場風險或不可分散風險，是影響所有資產的、不能通過資產組合來消除的風險。這部分風險是由那些影響整個市場的風險因素所引起的。這些因素包括宏觀經濟形勢的變動、國家經濟政策的變化、稅制改革、企業會計準則改革、世界能源狀況、政治因素等。 設為首頁
單項資產或資產組合受系統風險影響的程度，可以通過ß系數來衡量。
(一)單項資產的ß系數
單項資產的ß系數，是指可以反映單項資產收益率與市場平均收益率之間變動關系的一個量化指標。它表示單項資產收益率的變動受市場平均收益率變動的影響程度。換句話說，就是相對于市場組合的平均風險而言，單項資產系統風險的大小。
ß系數的定義式如下：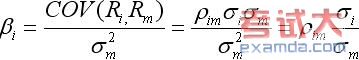
式中，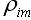
，表示第i種資產的收益率與市場組合收益率的相關系數;
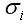是第i種資產收益率的標準差，表示該資產的風險大小;
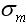是市場組合收益率的標準差，表示市場組合的風險;
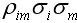三個指標的乘積表示第i種資產收益率與市場組合收益率的協方差。
由于無風險資產的 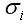為零，所以，無風險資產的β值為零;
市場組合相對于它自己的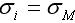 
，相關系數為1，所以，市場組合相對于它自己的β值為1。
(二)市場組合及其風險的概念
市場組合，是指由市場上所有資產組成的組合。它的收益率就是市場平均收益率，實務中通常用股票價格指數的收益率來代替。而市場組合的方差則代表了市場整體的風險。由于包含了所有的資產，因此市場組合中的非系統風險已經被消除，所以市場組合的風險就是市場風險。
①當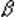 
=1時，表示該單項資產的收益率與市場平均收益率呈相同比例的變化，其風險情況與市場投資組合的風險情況一致;
②如果 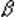>1，說明該單項資產的風險大于整個市場投資組合的風險;
③如果 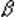<1，說明該單項資產的風險程度小于整個市場投資組合的風險。
