1、回歸分析的概念

所謂回歸分析，就是根據相關關系的具體形態，選擇一個合適的數學模型，來近似地表達變量間的依賴關系。

回歸分析和相關分析，聯系密切，有共同研究對象，在具體應用時，也常常需要互相補充。相關分析需要依靠回歸分析來表明現象數量相關的具體形式，而回歸分析則需要依靠相關分析來表明現象數量變化的相關程度。只有當變量之間存在著高度相關時，進行回歸分析尋求其相關的具體形式才有意義。

相關分析研究變量之間相關的方向和相關的程度；回歸分析研究變量之間相互關系的具體形式。

回歸分析過程：確定因變量X，自變量Y，用X來表示Y。

2、一元線性回歸模型

一元線性回歸方程：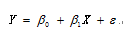

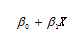反映了由于自變量X的變化而引起的因變量Y的線性變化。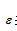表示線性關系之外的隨機因素，是個隨機變量。

因變量Y的期望E(Y)依賴自變量X的方程：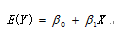

3、最小二乘法

4、模型的檢驗和預測

①模型的檢驗：決定系數，可以測度回歸直線對樣本數據的擬合程度，計算公式如下：

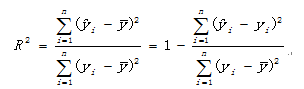
決定系數的取值在0到1之間。越接近1，擬合效果越好，越接近0，擬合效果越差。

②模型的預測：回歸分析的一個重要應用就是預測，即利用估計的回歸模型預估因變量數值。