二、簡答題(本大題共5小題,每題7分,共35分)
9.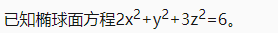
(1)求橢圓面上M(1,1,1)的切平面方程;(4分)
(2)當(dāng)k為何值時(shí),(1)中所求的切面與平面5x+ky-4z=0互相垂直。(3分)

10.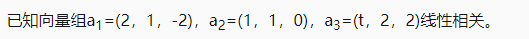
(1)求t的值;(4分)
(2)求該向量組的一個(gè)極大線性無關(guān)組,并將其余向量用極大無關(guān)組線性表示。(3分)

11.有甲、乙兩種品牌的某種飲料,其顏色、氣味及味道都極為相似,將飲料放在外觀相同的6個(gè)杯子中,每種品牌各3杯,作為試驗(yàn)樣品。
(1)從6杯樣品飲料中隨機(jī)選取3杯作為一次試驗(yàn),若所選飲料全部為甲種品牌,視為成功。獨(dú)立進(jìn)行5次試驗(yàn),求3次成功的概率;(5分)
(2)某人聲稱他通過品嘗飲料能夠區(qū)分這兩種品牌。現(xiàn)請(qǐng)他品嘗試驗(yàn)樣品中的6杯飲料進(jìn)行品牌區(qū)分,作為一次試驗(yàn),若區(qū)分完全正確,視為試驗(yàn)成功。他經(jīng)過5次試驗(yàn),有3次成功,可否由此推斷此人具有品嘗區(qū)分能力?說明理由。(2分)

(2)該品嘗者具備區(qū)分能力。
由(1)可知此隨機(jī)試驗(yàn)成功的概率大概為千分之一,是小概率事件,基本可以排除偶然性,故此人具備區(qū)分兩種品牌飲料的能力。
12.《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)》(實(shí)驗(yàn))用行為動(dòng)詞“了解”,“理解”,“掌握”,“應(yīng)用”等描述知識(shí)與技能目標(biāo),請(qǐng)解釋“了解函數(shù)奇偶性”的具體含義。
《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)》(2011年版)明確指出:了解是從具體實(shí)例中知道或舉例說明對(duì)象的有關(guān)特征;根據(jù)對(duì)象的特征,從具體情境中辨認(rèn)或者舉例說明對(duì)象。因此,“了解函數(shù)的奇偶性”要求學(xué)生能夠知道函數(shù)奇偶性,知道奇函數(shù)定義域和函數(shù)圖象都關(guān)于原點(diǎn)對(duì)稱的特點(diǎn),且有函數(shù)式子ƒ(-x)=- ƒ(x)成立;知道偶函數(shù)定義域關(guān)于原點(diǎn)對(duì)稱,圖象關(guān)于Y軸對(duì)稱,且有函數(shù)式子ƒ(-X)= ƒ(x)成立;學(xué)生能夠從具體函數(shù)例子中分辨哪些是奇函數(shù)哪些是偶函數(shù)。
13.書面測驗(yàn)是考量學(xué)生課程目標(biāo)達(dá)成狀況的重要方式,以“數(shù)列”一章為例,說明設(shè)計(jì)數(shù)學(xué)書面測驗(yàn)試卷應(yīng)關(guān)注的主要問題。
(1)學(xué)生在學(xué)習(xí)數(shù)列這一章的時(shí)候應(yīng)該掌握數(shù)列的概念,等差數(shù)列的概念、等差數(shù)列的通項(xiàng)公式及前n項(xiàng)和,等比數(shù)列的概念、等比數(shù)列的通項(xiàng)公式及前n項(xiàng)和。在設(shè)計(jì)題型的時(shí)候,考查的知識(shí)點(diǎn)應(yīng)包括以上知識(shí)點(diǎn),達(dá)到全面性,以便宏觀了解學(xué)生對(duì)本章知識(shí)的掌握程度。
(2)題型練習(xí)多樣化,可以設(shè)置選擇、填空、判斷、解答多種形式;試題的難度要有梯度,照顧到不同學(xué)習(xí)層次的學(xué)生,以便了解全體學(xué)生對(duì)本章知識(shí)掌握的程度,指導(dǎo)今后的教學(xué)工作。
(3)題目設(shè)置在檢測學(xué)生掌握本章知識(shí)的基礎(chǔ)上,應(yīng)有對(duì)重難點(diǎn)、易錯(cuò)點(diǎn)的考查。比如說“倒序相加法”“錯(cuò)位相減法”“裂項(xiàng)相消法”。
考后關(guān)注>>2017年教師資格證成績查詢時(shí)間 筆試多少分合格?

掃一掃,考試真題答案一手全掌握!
筆試一次過:告別盲目備考,講師為你講解90%必考點(diǎn),點(diǎn)擊進(jìn)入>>
備戰(zhàn)面試:2017年教師資格證面試考什么?講師為你還原面試現(xiàn)場>>

