五、案例分析題(本大題1小題,共20分)
16.案例:
在學習“平面向量”后,某數學教師安排了如下一道選擇題:
若非零向量a,b滿足|a-b|=|b|,則( )
A.|2b|>| a-2b|
B.|2b|<|a-2b|
C.|2a|>|2a-b|
D.|2a|<|2a-b|
以下是三位學生的解法:

問題:
(1)如果你是這位數學老師,請指出這二種解法存在的錯誤;(9分)
(2)請你從已知條件|a-b|=| b |出發,通過數形結合,引導學生給出一種正確的解法;(5分)
(3)針對學生在向量運算中的錯誤,請寫出實數運算與向量運算的不同點(至少寫出三點)。(6分)
(1)學生1在解答過程中只關注了a-b與b同向或反向時,在兩個向量模長相等時n與b滿足的關系,但是忽略了a-b與b兩個向量不共線的情況。學生2在解答過程中雖然注意到向量模長的性質,即|a|2=a·a,但是在化簡過程中把向量的數量積與實數的乘法產生了混淆。學生3在解答過程中忽略了向量數量積的性質,即a·b=| a|·| b|cosθ,其中θ為兩向量的夾角。
(2)向量的線性運算不僅涉及向量的長度還涉及向量的方向,因此提出以下問題串引導學生思考:
問題1:向量在進行線性運算加減法的時候,滿足什么樣的運算法則呢?
問題2:三角形法則與平行四邊形法則,兩種法則在計算過程中應根據向量的何種特征進行合理地選擇呢?
問題3:現在我們將a與b分兩種情況進行討論:①兩向量共起點時,②兩向量首尾相連時,兩種情況下分別對兩個向量進行減法的線性運算。現在大家動起手來一起在紙上畫一畫a與b滿足何種位置關系時,能夠使得|a-b|=|b|。我們又可以借助哪些特殊的圖形對兩個向量的位置關系進行描述呢?
問題4:兩種情況最終都可以用等腰三角形這樣的圖形進行概括描述,如圖,在等腰三角形ABC
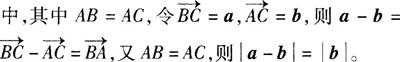
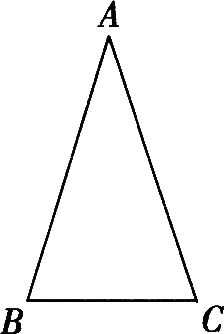
那么接下來,大家繼續借助等腰三角形ABC,在其基礎上畫出2b與a-2b,那么你可以發現什么結論呢?繼續畫出2a與2a-b,那么你又可以發現什么結論呢?
結論:根據三角形內任意兩邊和大于第三邊可以得出| 2b|>|a-2b|,2a與2a-b的關系無法判斷,應選A。
(3)向量運算與實數運算的本質區別在于,向量運算不僅涉及向量的長度,還涉及向量的方向。
向量的線性運算與實數運算雖然在運算過程中均滿足:交換律、結合律、分配律,但是向量線性運算結果為向量,實數的運算結果為實數。
向量的數量積與實數運算雖然在運算過程中均滿足:交換律、分配律且運算結果均為實數,但實數的乘法滿足消去律,向量的數量積則不滿足。在實數運算中若a≠0且ab=0則b=0,但在向量運算中若a≠0且a·b=0,則有兩種情況b=0或a⊥b。
考后關注>>2017年教師資格證成績查詢時間 筆試多少分合格?

掃一掃,考試真題答案一手全掌握!

