16、根據以下案例,回答后面的問題。
教學過程:
習舊引新
(1)在⊙O上,任取三個點A、B、C,然后順次連接,得到的是什么圖形?這個圖形與⊙O有什么關系?
(2)由圓內接三角形的概念,能否得出什么是圓的內接四邊形呢(類比)?
概念學習
(1)什么叫圓的內接四邊形?
(2)如圖1,說明四邊形ABCD與⊙O的關系。
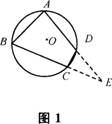
探討性質
(1)前面我們已經學習了一類特殊四邊形——平行四邊形,矩形,菱形,正方形,等腰梯形的性質,那么要探討圓內接四邊形的性質,一般要從哪幾個方面入手?
(2)打開《幾何畫板》,讓學生動手任意畫⊙O和⊙O的內接四邊形ABCD。(教師適當指導)
(3)量出所有值(圓的半徑和四邊形的邊,內角,對角線,周長,面積),并觀察這些量之間的關系。
(4)改變圓的半徑大小,這些量有無變化?由(3)觀察得出的某些關系有無變化?
(5)移動四邊形的一個頂點,這些量有無變化?由(3)觀察得出的某些關系有無變化?移動四邊形的四個頂點呢?移動三個頂點呢?
(6)如何用命題的形式表述剛才的實驗得出來的結論呢?(讓學生回答)
性質的證明及鞏固練習
(1)證明猜想
(2)完善性質
①若將線段BC延長到E,那么,∠DCE與∠BAD又有什么關系呢?
②圓的內接四邊形的性質定理:圓內接四邊形的對角互補,并且任何一個外角都等于它的內對角。
(3)練習。
例題講解
小結:為了使學生對所學的內容有一個完整而深刻的印象,讓學生組成小組,從概念,性質,方法,特殊性進行討論,然后對討論的結果進行歸納。
(1)本節課我們學習了圓內接四邊形的概念及圓內接四邊形的主要性質,要求同學們理解圓
內接四邊形和四邊形的外接圓的概念,理解圓內接四邊形的性質定理,并初步應用性質定理進行有關命題的證明和計算。
(2)我們結合《幾何畫板》的使用導出了圓內接四邊形的性質,在這一過程中用到了許多數學方法(實驗,觀察,類比,分析,歸納,猜想等),同學們要逐步學會并應用這些方法去探討有關的數學問題,提高我們的數學實踐能力與創新能力。
問題:(1)一般數學概念的學習包括哪幾個方面的內容?
(2)概念的獲取一般有哪些形式?
(3)談談你對該案例的看法。專題推薦:2014年各學科教學能力試題 深入考點
真題推薦:2014上半年學科知識與教學能力真題 233網校真題解析班,全面分析考卷!

