五、案例分析題(本大題1小題,共20分)
16.案例:
在一次數學課上,教師給出如下例題

正當老師要轉入下一個例題的時候.有學生提出:能否從等式右邊推導出等式左邊?教師以從等式右邊推導出左邊比較繁瑣為理由,不理會學生,就匆匆進入了下一個例題的講解。
問題:
(1)結合上述案例,談一談教師應如何看待學生提問不在教學預設的情況。(10分)
(2)如果你是該教師,那么如何回答學生的提問?(10分)
(1)教師應該區別對待學生提出的問題。首先,要判斷學生問題的價值,依據價值性大小給與回應。我們把與教學目標相關的問題都歸為“正問題”。把偏離或背離教學目標的問題歸為“負問題”。如本案例中學生的提問“能否從等式右邊推導出等式左邊”這一問題便是“正問題”,對待“正問題”應該給與積極回應。對學生提出的“負問題”,教師一方面可以啟發引導,將其轉化成“正問題”進行處理,一方面可以采取“冷處理”的辦法。其次,要依據問題的內容靈活進行,如師生互動討論或生生小組討論,也可以讓學生自行探究或課下解決。
(2)如果我是該教師我會將該問題作為一道思考題目,讓學生進行小范圍的討論,最后對此三種解題方式進行分析總結。具體實施方式如下:
問題1:剛剛這位同學提出了一個很新穎的解題思路。那么我們可不可以從等式右邊推導出等式左邊呢?大家同桌之間討論一下,可不可以,又是如何推導的呢?
我將在學生討論的過程中,進行巡視并對有問題的學生加以指導,為了不耽誤課堂進度,討論時間初步預設為3分鐘。
提問,請學生進行結果展示
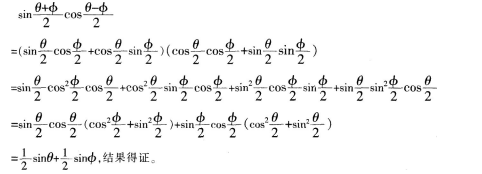
提問:對比三種解決方法,各自的優點是什么?談一談你更傾向于用哪種方法解決問題?
引導學生共同總結:在解決三角函數公式證明題的時候,①合理的選擇誘導公式以及和差化積公式非常的重要,如:方法三對于兩角和差公式的反復運用,雖計算過程稍微復雜,但是方法更加的簡單,容易想到。②能夠靈活的運用整體代換的思想方法快速解決問題,如:方法一、方法二可以精簡計算過程,避免計算出錯。
查分關注>>2016下半年教師資格證成績查詢時間 合格分數線 成績有效期
筆試,下次一定過:告別盲目備考,講師為你講解90%必考點,點擊進入>>
提前備戰面試:2016年教師資格證面試考什么?講師為你還原面試現場>>

