5.基本系數

　　一次支付本利和因數(F/P，i，n)

　　一次支付現值因數(P/F，i，n)

　　等額支付將來值因數(F/A，i，n)

　　等額支付償債基金因數(A/F，i，n)

　　等額支付現值因數(P/A，i，n)

　　等額支付資金回收因數(A/P，i，n)

　　1.一次性支付本利和公式

　　問題：已知現期的一個支付，在一定利率條件下，求未來某時點的將來值。即已知P、i、n，求F。圖示如下：

　　這就是一般復利公式

　　應用分析

　　某夫婦喜得貴子之時，即投入一筆大學教育基金10000元，以年均5%的收益率投資，當孩子18歲上大學時，這筆基金會有多少呢?

　　解析:

　　F = 10000(F/P,5%,18)

　　= 10000×2.407

　　=24070(元)

　　2.一次性支付現值公式

　　問題：已知將來某個時點的一個支付，在一定利率條件下，求其現在值。即已知F、i、n，求P。圖示如下：

　　它是一般復利公式的逆公式

　　應用分析

　　某夫婦喜得貴子之時，考慮投入一筆基金用于大學教育，預計孩子18歲上大學時所需各種費用為50000元，設年均收益率為8%,問現在應投入多少?

　　解析：?

　　P = 50000(P/F,8%,18)

　　= 50000×0.2502

　　= 12510(元)

　　3.等額支付將來值公式

　　問題：已知到將來某個時點的各期均有一個等額支付，在一定利率條件下，求其將來值。

　　即已知A、i、n，求F。圖示如下：

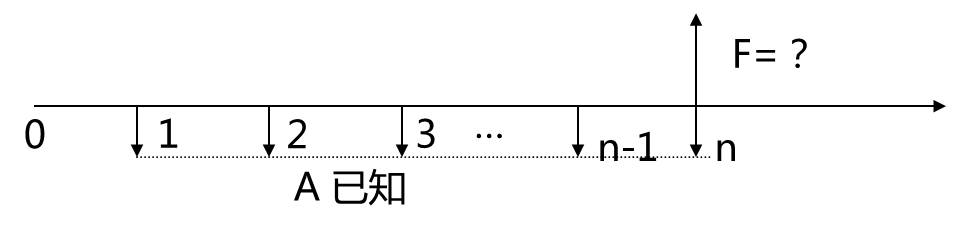
　　計算公式可由一般復利公式 F = P(1+ i) n推導出來

　　應用分析

　　某夫婦喜得貴子之時，考慮建立一項基金用于大學教育，計劃每年注入2000元，至孩子18歲上大學時會有多少?設年均收益率為8%。

　　解析：

　　F = 2000(F/A,8%,18)

　　= 2000×37.45

　　= 74900(元)

　　4.償債基金公式

　　問題：已知到將來某個時點的一個支付，在一定利率條件下，求從現在起到該時點各期的等額支付。即已知F、i、n，求A。圖示如下：

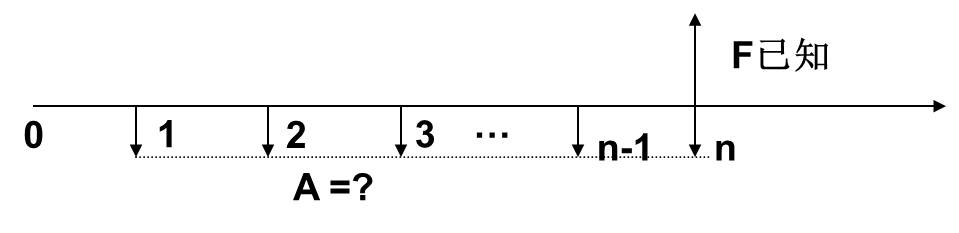
　　計算公式可由年金本利和公式推導而來

　　應用分析

　　某夫婦喜得貴子之時，考慮建立一項基金用于大學教育，預計孩子18歲上大學時所需各種費用為50000元，設年均收益率為8%，問從現在起每年應投入多少?

　　解析：

　　A = 50000(A/F,8%,18)= 50000×0.0267=1335(元)