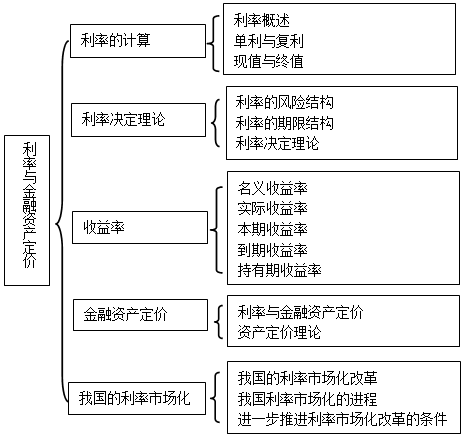
2016年中級經濟師考試金融專業第二章核心考點
計算各種利率,理解利率風險結構、利率期限結構和利率決定理論,計算各種收益率,理解和進行金融資產定價,科學分析我國的利率市場化。
節 利率的計算
一、利率概述
利率是指借款人在單位時間內應支付的利息同借貸資金的比率,這里的利息是資金所有者由于借出資金而取得的報酬。
利率的分類:
①按利率的決定方式可劃分為固定利率與浮動利率;
②按利率的真實水平可劃分為名義利率與實際利率;
③按計算利率的期限單位可劃分為年利率、月利率、日利率。
年利率=月利率×12=日利率×360
二、單利與復利
1.單利
單利就是不論借貸期限的長短,僅按本金計算利息,上期本金所產生的利息不計入下期本金計算利息。單利計算公式為:
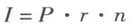
其中,I表示利息,P表示本金,r表示利率,n表示時間。
根據中國人民銀行規定的計息規則,在我國,活期儲蓄存款按復利,每個季度計息,定期存款、定活兩便、零存整取、整存整取、整存零取等其他儲蓄存款是按單利計息的。
【例2.1】某投資者購買了10000元的投資理財產品,期限2年,年利率為6%,按年支付利息。假定不計復利,年收到的利息也不用于再投資,則該理財產品到期時的本息和為( )元。
A.10600.00
B.11200.00
C.11910.16
D.11236.00
【答案】B
【解析】單利計算公式為:I=P×r×n。其中,I表示利息額,P表示本金,r表示利率,n表示時間。則該理財產品到期時的本息和為:FV=10000+10000×6%×2=11200(元)。
2.復利
(1)普通復利
復利也稱利滾利,就是將每一期所產生的利息加入本金一并計算下一期的利息。復利的計算公式為:
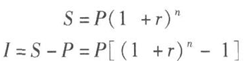
其中,S為本息和,表示利息額,P表示本金,r表示利率,n表示時間。
若本金為P,年利率為r,每年的計息次數為m,則第n年末的本息和為:
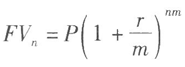
(2)連續復利
在公式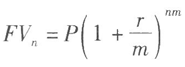 中,如果m趨于∞,則
中,如果m趨于∞,則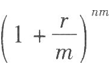 趨于em,其中e約等于2.71828。因此,對于本金以連續復利計算n年末的本息和,得到:
趨于em,其中e約等于2.71828。因此,對于本金以連續復利計算n年末的本息和,得到:
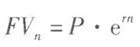
每年的計息次數越多,終的本息和越大,隨計息間隔的縮短,本息和以遞減的速度增加,后等于連續復利的本息和。
三、現值與終值
現值,也稱在用價值,現值是現在和將來(或過去)的一筆支付或支付流在今天的價值。
1.系列現金流的現值
一般地,系列現金流的現值可由下面的公式得到:
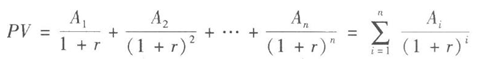
其中,Ai表示第i年末的現金流量,r是年貼現率。
2.連續復利下的現值
假如一年之內多次支付利息,則利息率為r/m,此時現值的計算公式為:
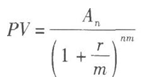
其中,An表示第n年末的現金流量,m是年計息次數,r是貼現率。
上式中,如果m趨于∞,則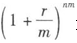 趨于em,因此,如果是連續復利,則:
趨于em,因此,如果是連續復利,則:
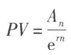
每年的計息次數越多,現值越小,隨計息間隔的縮短,現值以遞減的速度減小,后等于連續復利條件下的現值。
【例2.2】某機構投資者計劃進行為期2年的投資,預計第2年年末收回的現金流為121萬元。如果按復利每年計息一次,年利率10%,則第2年年末收回的現金流現值為( )萬元。
A.100
B.105
C.200
D.210
【答案】A
【解析】現值是指未來某一時點上的一定量現金折合到現在的價值,俗稱“本金”。連續復利下的現值的計續復利下的現值的計算公式為: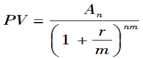 ,式中,An表示第n年末的現金流量,m是年計息次數,r是年貼現率。所以,第2年年末收回的現金流現值為121/(1+10%)2=100(萬元)。來源233網校
,式中,An表示第n年末的現金流量,m是年計息次數,r是年貼現率。所以,第2年年末收回的現金流現值為121/(1+10%)2=100(萬元)。來源233網校
3.終值及其計算
(1)定義
終值,又稱將來值或本息和,是指現在一定量的資金在未來某一時點上的價值。
(2)計算方式
①單利。假如當前有一筆資金,共計金額為P,存期為n年,年利率為r,如果按單利計算,則n年后的終值FVn為:
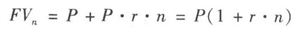
②復利。設現有一筆資金,共計金額為P,存期為n年,年利率為r,如果每年復利一次,則n年后的終值FV為:
FV=P(1+r)N
其中(1+r)n稱為復利終值系數。
難度分析:2016年中級經濟師考試金融特點分析
章節講義:2016年中級經濟師金融章節講義匯總
背誦考點:2016年中級經濟師考試金融知識點匯總
相關推薦
- 2016年中級金融核心考點匯總09-28
- 2016年中級金融第十章核心考點09-27
- 2016年中級金融第九章核心考點09-27
- 2016年中級金融第八章核心考點09-27
- 2016年中級金融第七章核心考點09-26
| ?γ??????? | ??? | ???/???? | ??????? | ???? |
|---|---|---|---|---|
| 2017???м???????????????? | ?????? | ??350 / ??350 |  |
???? |
| 2017???м?????????? | ?????? | ??350 / ??350 |  |
???? |
| 2017???м????????????????? | ?????? | ??350 / ??350 |  |
???? |
| 2017???м????????????? | ????? | ??350 / ??350 |  |
???? |
| 2017???м????????????? | ????? | ??350 / ??350 |  |
???? |
| 2017???м???????????????? | ??? | ??350 / ??350 |  |
???? |
| 2017???м?????????t????? | ??? | ??350 / ??350 |  |
???? |
| 2017???м???????????t????? | κ???? | ??350 / ??350 |  |
???? |