二、幾何布朗運動

　　1.幾何布朗運動的定義

　　幾何布朗運動(GBM) (也叫做指數(shù)布朗運動) 是連續(xù)時間情況下的隨機過程，其中隨機變量的對數(shù)遵循布朗運動. 幾何布朗運動在金融數(shù)學(xué)中有所應(yīng)用，用來在布萊克-舒爾斯定價模型中模仿股票價格。法國數(shù)學(xué)家巴舍利耶在《投機交易理論》一文中提出股票價格遵循布朗運動。保羅·薩繆爾森1965年首次提出了股價S應(yīng)遵循幾何布朗運動。

　　2.相關(guān)方程式

　　1)股價S的隨機微分方程形式為：

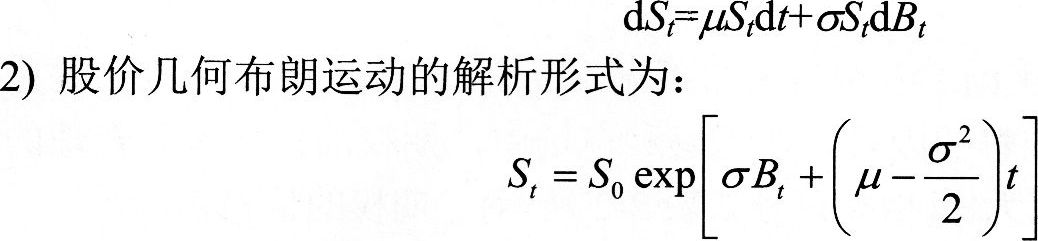
　　上式中，S表示t時刻的股價，μ、σ為常量，分別表示股票的期望收益率和波動率，Bt服從標(biāo)準(zhǔn)布朗運動。從公式可以看出，股票價格在短時期內(nèi)的變動(即收益)來源于兩個方面：①短時間內(nèi)的預(yù)期收益率的變化;②隨機正態(tài)波動項。

　　3、應(yīng)用：

　　幾何布朗運動在布萊克-舒爾斯定價模型被用來定性股票價格，因而也是最常用的描述股票價格的模型。使用幾何布朗運動來描述股票價格的理由:

　　幾何布朗運動的期望與隨機過程的價格(股票價格)是獨立的, 這與我們對現(xiàn)實市場的期望是相符的。

　　幾何布朗運動過程只考慮為正值的價格, 就像真實的股票價格。

　　幾何布朗運動過程與我們在股票市場觀察到的價格軌跡呈現(xiàn)了同樣的“roughness” 。

　　幾何布朗運動過程計算相對簡單。.

　　然而，幾何布朗運動并不完全現(xiàn)實，尤其存在一下缺陷:

　　在真實股票價格中波動隨時間變化 (possiblystochastically), 但是在幾何布朗運動中, 波動是不隨時間變化的。

　　在真實股票價格中, 收益通常不服從正態(tài)分布 (真實股票收益有更高的峰度('fatter tails'), 代表了有可能形成更大的價格波動).