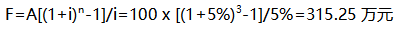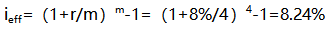一級建造師工程經(jīng)濟(jì)的考試,出題相對固化,存在高頻考點(diǎn),尤其是計(jì)算題的部分。所以在經(jīng)濟(jì)上的復(fù)習(xí),要吃透教材,掌握技巧,做到以不變應(yīng)萬變。
資金時(shí)間價(jià)值的計(jì)算及應(yīng)用一直以來都是一建經(jīng)濟(jì)考試計(jì)算題的高頻考點(diǎn),現(xiàn)在,就這部分的內(nèi)容做一個(gè)歸納與詳解,以便大家能更好地理解和掌握。
一、公式匯總

(注:只需要記住現(xiàn)值的公式即可,終值的公式可以根據(jù)終值和現(xiàn)值的關(guān)系推導(dǎo)出來)
二、資金時(shí)間價(jià)值的計(jì)算及應(yīng)用
1、利息
(1)單利(利不生利):在計(jì)算利息時(shí),僅用最初本金來計(jì)算,而不計(jì)入先前計(jì)息周期中所累積增加的利息。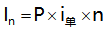
(2)復(fù)利(利生利,利滾利):在計(jì)算某一計(jì)息周期的利息時(shí),其先前周期上所累積的利息要計(jì)算利息。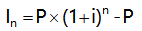
(本金越大,利率越高,計(jì)息周期越多時(shí),復(fù)利和單利的利息差距就越大)
三、資金等值計(jì)算及應(yīng)用
資金有時(shí)間價(jià)值,即使金額相同,因其發(fā)生在不同時(shí)間,其價(jià)值就不相同;反之,不同時(shí)點(diǎn)絕對數(shù)額不等的資金在時(shí)間價(jià)值的作用下卻可能具有相等的價(jià)值。
1、現(xiàn)金流量圖作圖方法規(guī)則(要學(xué)會畫圖,對做題的幫助很大)
(1)以橫軸為時(shí)間軸,0表示時(shí)間序列的起點(diǎn)即現(xiàn)在;時(shí)間軸上的點(diǎn)稱為時(shí)點(diǎn),通常表示該時(shí)間單位末的時(shí)點(diǎn)。
(2)相對于時(shí)間坐標(biāo)的垂直箭線代表不同時(shí)點(diǎn)的現(xiàn)金流量情況,現(xiàn)金流量的性質(zhì)是對特定的人而言的。(對投資人而言,橫軸上方表示現(xiàn)金流入,橫軸下方表示現(xiàn)金流出)。
(3)箭線的長短體現(xiàn)各時(shí)點(diǎn)現(xiàn)金流量數(shù)值大小的差異(不成比例)。
(4)箭線與時(shí)間軸的交點(diǎn)即為現(xiàn)金流量發(fā)生的時(shí)點(diǎn)(表示時(shí)間單位的末期)。

2、現(xiàn)金流量的三要素:現(xiàn)金流量的大小(現(xiàn)金流量數(shù)額)、方向(現(xiàn)金流入或流出)和作用點(diǎn)(現(xiàn)金流量發(fā)生的時(shí)點(diǎn))
四、終值和現(xiàn)值的計(jì)算

1、現(xiàn)值(P):資金發(fā)生在(或折算為)某一特性時(shí)間序列起點(diǎn)時(shí)的價(jià)值,即現(xiàn)在的資金價(jià)值或本金。
2、終值(F):資金發(fā)生在(或折算為)某一特性時(shí)間序列終點(diǎn)的價(jià)值,即n期末的資金價(jià)值或本利和。
3、年金(A):發(fā)生在(或折算為)某一特定時(shí)間序列各計(jì)息期末(不包括零期)的等額資金序列的價(jià)值。
4、公式
(1)一次支付的終值
F=P(1+i)n 或 F=P(F/P, i, n)
(2)一次支付的現(xiàn)值
P=F(1+i)-n 或 P=F(P/F, i, n)
(3)等額支付的終值
 或 F=A(F/A, i, n)
或 F=A(F/A, i, n)
(4)等額支付的現(xiàn)值
 或 P=A(P/A, i, n)
或 P=A(P/A, i, n)
【經(jīng)典例題】某投資項(xiàng)目,計(jì)算期5年,每年年末等額收回100萬元,問在年利率為10%時(shí),開始須一次投資多少?
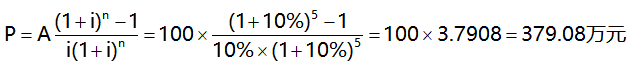
5、等值計(jì)算公式使用注意事項(xiàng)
(1)計(jì)息期數(shù)為時(shí)點(diǎn)或時(shí)標(biāo),本期末即等于下期初,0點(diǎn)就是第一期初;第一期末即等于第二期初,余類推。
(2)P是在第一計(jì)息期開始時(shí)(0期)發(fā)生。
(3)F發(fā)生在考察期期末,即n期末。
(4)各期的等額支付A,發(fā)生在各期期末。
(5)當(dāng)問題包括P與A時(shí),系列的第一個(gè)A與P隔一期,即P發(fā)生在系列A的前一期期末。
(6)當(dāng)問題包括A與F時(shí),系列的最后一個(gè)A與F是同時(shí)發(fā)生。不能把A定在每期期初,因?yàn)楣降慕⑴c它是不相符的。
【經(jīng)典例題】假設(shè)i=10%,現(xiàn)在的1000元等于5年末的多少元?
【解析】


五、有效利率的計(jì)算
有效利率為資金在計(jì)息中所發(fā)生的實(shí)際利率,包括計(jì)息周期有效利率和年有效利率兩種情況。
1、計(jì)息周期有效利率,即計(jì)息周期利率 i:i=r/m
2、年有效利率,公式:
(P:年初資金;r:名義利率;m:計(jì)息次數(shù))
注:年有效利率和名義利率的關(guān)系實(shí)質(zhì)上與復(fù)利和單利的關(guān)系一樣。每年計(jì)息周期m越多,兩者相差越大。
【經(jīng)典例題】每半年內(nèi)存款1000元,年利率8%,每季復(fù)利一次。問五年末存款金額為多少?
【解析】

計(jì)息期利率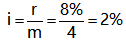
半年期實(shí)際利率 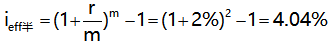

以上就是這部分的所有內(nèi)容了,現(xiàn)在就來做一些真題練習(xí)吧!加深對公式的理解和提高解題能力。
1、(2015)某企業(yè)第1年年初和第1年年末分別向銀行借款30萬元,年利率均為10%,復(fù)利計(jì)息,第3-5年年末等額本息償還全部借款。則每年年末應(yīng)償還金額為 ( )。
A.20.94
B.23.03
C.27.87
D.31.57
參考解析:此題為歷年考題中的代表性難題之一,這種難度的考題很少,所以不會做也不要被嚇到。
首先,將第0、1年末的30萬元,折算到第5年末,求終值F;然后再求3年內(nèi)(3~5)的等額資金

2、(2017)某施工企業(yè)年初從銀行借款200萬元,按季度計(jì)息并支付利息,季度利率為1.5%,則該企業(yè)一年支付的利息總計(jì)為 ( ) 萬元
A.6.00
B.6.05
C.12.00
D.12.27
參考解析:該筆借款按季度計(jì)息并支付利息,其計(jì)息周期和資金收付周期均為季度,故為單利計(jì)息。
一年支付的利息總計(jì)=200x1.5%x4=12.00萬元
3、(2016)某施工企業(yè)從銀行借款100萬元,期限3年,年利率8%,按年計(jì)息并于每年末付息,則第3年年末企業(yè)需償還的本利和為 ( ) 萬元。
A.100
B.108
C.124
D.126
參考解析:按年計(jì)息并于每年末付息,故為單利計(jì)息。
第三年的利息=100 x 8%=8萬元,本利和共計(jì)為8=108萬元。
4、(2019)某企業(yè)以單利計(jì)息的方式年初借款1000萬元,年利率6%,每年末支付利息,第五年末償還全部本金,則第三年末應(yīng)支付的利息為 ( ) 萬元。
A.300.00
B.180.00
C.71.46
D.60.00
5、(2018)某施工企業(yè)每年年末存入銀行100萬元,用于3年后的技術(shù)改造,已知銀行存款年利率為5%,按年復(fù)利計(jì)息,則到第3年末可用于技術(shù)改造的資金總額為 ( ) 萬元。
A.331.01
B.330.75
C.315.25
D.315.00