二、簡答題(本大題共5小題,每題7分,共35分)


(2) 在該變換條件下,①不變的性質:都是中心對稱圖形和軸對稱圖形,都是在某條件下點的軌跡所形成的對稱圖形;②變化的性質:圖形形態發生了變化,不再以原點為中心點,不再與x軸和y軸相交,圖形距離中心點的距離都相等。
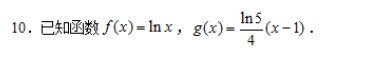
(1)求f(x)和g(x)圍成的平面區域的面積.
(2)求0≤y≤f(x), 1≤x≤3,繞y軸旋轉的體積.
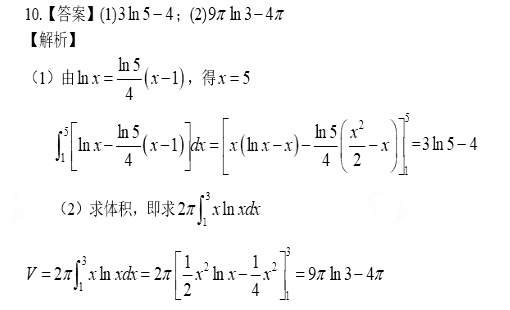
11.一個袋子里有8個黑球,8個白球,隨機不放回連續取球5次,每次取出1個球,求最多取到3個白球的概率.

12.給出數學文化的內容,請舉出數學課堂中兩個能夠應用數學文化的例子.
數學是一門與概念、定理、公式相關的學科,教師在數學教學中滲透數學文化、設置與教學內容相關的且蘊含在現實生活中的數學文化、引導學生思考其中所隱含的數學知識和規律,對學生的數學學習具有巨大的幫助。例如:
(1)在學習《整數和負數》時,“負數” 概念對學生來說相對抽象。教師可以在教學中滲透數學文化史:中國是最早提出負數的國家,《九章算術》 是最早、最完整介紹負數的古書,人們在求解方程時經常會遇到小數減大數的情形,為便于求解,便創造了負數;在古代為區分正負數,數學家創造了一種方法:用不同顏色的算籌來表示正、負數;中國古代不僅提出了負數的概念,還提出了整套的正、負數的運算法則,這些法則沿用至今。教師在教學中融入數學文化,讓學生了解概念產生的背景和意義,利用概念與生活的相通性可以幫助學生更直觀地理解概念。
(2)在教學《勾股定理》時,可以從畢達哥拉斯到朋友家做客的故事入手:畢達哥拉斯是古希臘最為著名的數學家之-,相傳2500年前,他到朋友家做客,發現朋友家用地板磚鋪成的地面反映出了直角三角形的三邊關系。畢達哥拉斯發現直角三角形的三邊關系的故事為《勾股定理》的教學提供了問題引入,學生通過思考故事中隱含的規律,從而進行猜想假設,再加上教師的演示將定理變得具體形象,學生能夠更容易地總結出直角三角形的三邊關系,即勾股定理。探究勾股定理相關的數學文化史的過程蘊含了豐富的數學思想方法,這對學生理解定理極為有利。
將數學文化滲透到數學教學中,將教材內容與數學文化巧妙結合起來,從數學文化中延伸出數學概念和規律,可以幫助學生理解相關內容。數學文化中蘊含的故事具有較強的趣味性,還可以激發學生的學習興趣。
13.簡述數學建模的主要過程.
數學建模是運用數學思想、方法和知識解決實際問題的過程。建立和求解模型的過程包括:從現實生活或具體情境中抽象出數學問題,用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律,求出結果、并討論結果的意義。具體如下:
(1)模型準備:了解問題的實際背景,明確其實際意義,掌握對象的各種信息。以數學思想來包容問題的精髓,數學思路貫穿問題的全過程,進而用數學語言來描述問題。要求符合數學理論,符合數學習慣,清晰準確。
(2)模型假設:根據實際對象的特征和建模的目的,對問題進行必要的簡化,并用精確的語言提出一-些恰當的假設。
(3)模型建立:在假設的基礎上,利用適當的數學具來刻劃各變量常量之間的數學關系,建立相應的數學結構(盡量用簡單的數學工具)。
(4)模型求解:利用獲取的數據資料,對模型的所有參數做出計算(或近似計算)。
(5)模型分析:對所要建立模型的思路進行闡述,對所得的結果進行數學上的分析。
(6)模型檢驗:將模型分析結果與實際情形進行比較,以此來驗證模型的準確性、合理性和適用性。如果模型與實際較吻合,則要對計算結果給出其實際含義,并進行解釋。如果模型與實際吻合較差,則應該修改假設,再次重復建模過程。
下載233網校APP及時獲取2019下半年教師資格證考試真題
面試報考:2019下半年教師資格證面試報名時間
教師資格證面試如何快速通關?面試情景還原,助你一舉攻下“結構化面試+試講+答辯”三大內容,實戰通關!試聽課程>>


