（二）資本資產定價模型的應用

　　1.證券市場線對證券市場的描述

　　市場風險溢酬（R_m一R_f）反映的是市場整體對風險的偏好，如果風險厭惡程度高，則市場風險溢酬的值就大，那么當某項資產的系統風險水平（用β表示）稍有變化時，就會導致該項資產的必要收益率以較大幅度變化；相反，如果多數市場參與者對風險的關注程度較小，那么資產的必要收益率受其系統風險的影響則較小。

　　當無風險收益率上漲而其他條件不變時，所有資產的必要收益率都會上漲同樣的數量；反之，當無風險收益率下降且其他條件不變時，所有資產的必要收益率都會下降同樣的數量。

　　2.證券市場線與市場均衡

　　資本資產定價模型認為，證券市場線是一條市場均衡線，市場在均衡的狀態下，所有資產的預期收益都應該落在這條線上。也就是說，在均衡狀態下，每項資產的預期收益率應該等于其必要收益率，其大小由證券市場線的核心公式來決定。

　　在資本資產定價模型的理論框架下，假設市場是均衡的，則資本資產定價模型還可以描述為：

　　預期收益率＝必要收益率＝R_f＋β×（R_m一R_f）

　　3.資本資產定價模型的有效性和局限性

　　資本資產定價模型和證券市場線最大的貢獻在于它描述了風險與收益之間的數量關系，首次將“高收益伴隨著高風險”的直觀認識，用簡單的關系式表達出來。

　　但在實際運用中，該模型仍存在著一些明顯的局限，主要表現在：（1）某些資產或企業的β值難以估計，對于那些缺乏歷史數據的新興行業而言尤其如此；（2 ） 即使有充足的歷史數據可以利用，但由于經濟環境的不確定性和不斷變化，使得依據歷史數據估算出來的β值對未來的指導作用大打折扣；（3）資本資產定價模型和證券市場線是建立在一系列假設之上的，其中一些假設與實際情況有較大的偏差。

　　三、套利定價理論

　　套利定價理論（APT ） ，也是討論資產的收益率如何受風險因素影響的理論。所不同的是，套利定價理論認為資產的預期收益率并不是只受單一風險的影響，而是受若干個相互獨立的風險因素，如通貨膨脹率、利率、石油價格、國民經濟的增長指標等的影響，是一個多因素的模型。

　　該模型的基本形式為：

　　E（R）＝R_f^*＋b₁λ₁＋b₂λ₂＋…＋b_nλ_n

　　式中，E（R）表示某項資產的預期收益率；R_f^*表示不包括通貨膨脹因素的無風險收益率，即純利率；b_i表示風險因素i對該資產的影響程度，稱為資產對風險因素i 的響應系數；λ_i表示風險因素i的預期收益率，即該資產由于承擔風險因素i而預期獲得的收益率。

　　第三章　資金時間價值與證券評價

　[ 基本要求］

　　（一）掌握復利現值和終值的含義與計算方法

　　（二）掌握年金現值、年金終值的含義與計算方法

　　（三）掌握利率的計算，名義利率與實際利率的換算

　　（四）掌握股票收益率的計算，普通股的評價模型

　　（五）掌握債券收益率的計算，債券的估價模型

　　（六）熟悉現值系數、終值系數在計算資金時間價值中的運用

　　（七）熟悉股票和股票價格

　　（八）熟悉債券的含義和基本要素

　　[考試內容]

　　第一節 資金時間價值

　　一、資金時間價值的含義

　　資金時間價值，是指一定量資金在不同時點上的價值量差額。資金的時間價值來源于資金進入社會再生產過程后的價值增值。通常情況下，它相當于沒有風險也沒有通貨膨脹情況下的社會平均利潤率，是利潤平均化規律發生作用的結果。

　　根據資金具有時間價值的理論，可以將某一時點的資金金額折算為其他時點的金額。

　　二、現值與終值的計算

　　現值，是指未來某一時點上的一定量資金折算到現在所對應的金額，通常記作P₀ 終值又稱為將來值，是現在一定量的資金折算到未來某一時點所對應的金額，通常記作F₀

　　現值和終值概念可以適當推廣。對于所分析的任意一段時間，資金在起始時刻的價值量都可以稱為現值；資金在終了時刻的價值量都可以稱為終值。一定量資金的終值與現值的差額即為資金的時間價值；連接現值和終值并實現兩者相互折算的百分數稱為折現率。現實生活中“本金”、“本利和”的說法相當于資金時間價值理論中的“現值”和“終值”概念，利息和利率類似于資金時間價值的絕對數和相對數形式，利率經常被當作折現率使用。現值和終值對應的時點之間可以劃分為若干個計息周期。

　　（一）現值和終值的基本計算

　　利息的計算有單利和復利兩種方式，在不同的計息方式下，現值和終值之間的數量關系不同。通常情況下，資金時間價值采用復利計息方式進行計算。

　　1.單利計息方式下現值與終值的關系　
　　

　　

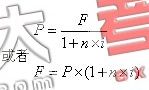
　　（二）年金現值和年金終值的計算

　　如果多期發生現金流，則每期現金流均按現值和終值的基本公式計算。多期現金流的一種特殊情況是，現金流入（或者流出）間隔的時間相同、金額相等，這種類型的系列現金流稱為年金，每期流入（或流出）的金額用A表示。年金按其每次收付發生的時點不同，可分為普通年金、即付年金、遞延年金、永續年金等。

　　1.普通年金的現值和終值的計算

　　普通年金又稱后付年金，是指從第1期起，在一定時期內每期期末等額收付的系列款項。普通年金有時也簡稱年金。

　　（1）普通年金的現值計算公式與現值系數　
　　

　　2.即付年金現值系數和終值系數

　　即付年金又稱先付年金，是指從第1 期起，在一定時期內每期期初等額收付的系列款項。即付年金與普通年金的區別在于，即付年金的收付行為發生在每期期初，而普通年金的收付行為發生在每期期末。

　　即付年金現值系數＝（1+i）×普通年金現值系數

　　即付年金終值系數＝（1+i）×普通年金終值系數

　　3.遞延年金

　　如果在所分析的期間中，前m 期沒有年金收付，從第m +1期開始形成普通年金，這種情況下的系列款項稱為遞延年金。計算遞延年金的現值可以先計算普通年金現值，然后再將該現值視為終值，折算為第1期期初的現值。遞延年金終值與普通年金終值的計算相同。

　　4.永續年金

　　普通年金的期數n 趨向于無窮大時形成永續年金。永續年金不計算終值。

　　

　　（三）現值與終值系數表

　　顯然，現值、終值系數的所有公式都只需要三個因素：計息方式、每期利率和期數。在復利計息方式下，由不同利率i和期數n 的組合計算出各種情況下的現值和終值系數，并依照一定順序排列成復利現值系數表、復利終值系數表、年金現值系數表、年金終值系數表等。在計算資金的時間價值時，只需要根據i ，n 兩個因素查詢相應表格，即可獲得有關現值系數和終值系數。

　　三、利率的計算

　　（一）復利計息方式下利率的計算

　　利率、現值（或者終值）系數之間存在一定的數量關系。已知現值（或者終值）

　　系數，則可以通過內插法公式計算出對應的利率：

　　

　　1.若已知復利現值（或者終值）系數B 以及期數n可以查“復利現值（或者終值）系數表”，找出與已知復利現值（或者終值）系數最接近的兩個系數及其對應的利率，按內插法公式計算出利率。

　　2.若已知年金現值（或者終值）系數B 以及期數幾可以查“年金現值（或者終值）系數表”，找出與已知年金現值（或者終值）系數最接近的兩個系數及其對應的利率，按內插法公式計算出利率。

　　3.永續年金的利率可以通過公式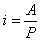， 計算得出。

　　（二）名義利率與實際利率

　　如果以“年”作為基本計息期，每年計算一次復利，這種情況下的年利率為名義利率。如果按照短于1 年的計息期計算復利，并將全年利息額除以年初的本金，此時得到的利率則為實際利率。名義利率與實際利率的換算關系如下：

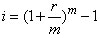
　　式中，i實際利率；r名義利率；m為每年復利次數。

　　第二節 普通股及其評價

　　一、股票與股票收益率

　　（一）股票的價值與價格

　　股票，是股份公司發行的、用以證明投資者的股東身份和權益，并據以獲得股利的一種可轉讓的證明。

　　1.股票的價值形式

　　股票的價值形式有票面價值、賬面價值、清算價值和市場價值。

　　2.股票的價格

　　股票價格有廣義和狹義之分。狹義的股票價格就是股票交易價格；廣義的股票價格則包括股票的發行價格和交易價格兩種形式。股票交易價格具有事先的不確定性和市場性特點。

　　3.股價指數

　　股價指數，是指金融機構通過對股票市場上一些有代表性的公司發行的股票價格進行平均計算和報考對比后得出的數值，它是用以表示多種股票平均價格水平及其變動，并權衡股市行情的指標。股價指數的計算方法有簡單算術平均法、綜合平均法、幾何平均法和加權綜合法等。

　　（二）股票的收益率

　　股票的收益，是指投資者從購入股票開始到出售股票為止整個持有期間的收入，由股利和資本利得兩方面組成。

　　股票收益率是股票收益額與購買成本之比。為便于與其他年度收益指標相比較，可折算為年均收益率。股票收益率主要有本期收益率、持有期收益率兩種。

　　本期收益率，是指股份公司上年派發的現金股利與本期股票價格的比率，反映了以現行價格購買股票的預期收益情況。

　　

　　式中，年現金股利是指上年發放的每股股利；本期股票價格是指該股票當日證券市場收盤價。

　　持有期收益率，是指投資者買入股票持有一定時期后又將其賣出，在投資者持有該股票期間的收益率，反映了股東持有股票期間的實際收益情況。

　　如投資者持有股票的時間不超過1 年，不考慮復利計息問題，其持有期收益率可按如下公式計算：

　　

　　二、普通股的評價模型

　　普通股的價值（內在價值）是由普通股產生的未來現金流量的現值決定的，股票給持有者帶來的未來現金流入包括兩部分：股利收入和股票出售時的資本利得。股票的價值由一系列的股利和將來出售股票時進、售價的差額所構成。其基本計算公式是：

　　　
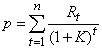
　　 式中，P 是股票價值；R_t是股票第t年產生的現金流入量（包括股利收入、賣出股票的資本利得）；K是折現率；n是持有年限。

　　（一）股利固定模型

　　如果長期持有股票，且各年股利固定，其支付過程即為一個永續年金，則該股票價值的計算公式為：　
　　　
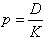
　　 式中，D為各年收到的固定股息；其他符號的含義與基本公式相同。

　　（二）股利固定增長模型

　　從理論上看，企業的股利不應當是固定不變的，而應當是不斷增長的。假定企業長期持有股票，且各年股利按照固定比例增長，則股票價值計算公式為：　
　　　　　
　　 （三）三階段模型

　　在現實生活中，有的公司股利是不固定的。如果預計未來一段時間內股利將高速增長，接下來的時間則為正常固定增長或者固定不變，則可以分別計算高速增長、正常固定增長、固定不變等各階段未來收益的現值，各階段現值之和就是股利非固定增長情況下的股票價值。

　　

　　（四）普通股評價模型的局限性

　　1.未來經濟利益流入量的現值只是決定股票價值的基本因素而不是全部因素，其他很多因素（如投機行為等）可能會導致股票的市場價格大大偏離根據模型計算得出的價值。

　　2.模型對未來期間股利流入量預測數的依賴性很強，而這些數據很難準確預測。股利固定不變、股利固定增長等假設與現實情況可能存在一定差距。

　　3.股利固定模型、股利固定增長模型的計算結果受D₀ 或D_l 的影響很大，而這兩個數據可能具有人為性、短期性和偶然性，模型放大了這些不可靠因素的影響力。

　　4.折現率的選擇有較大的主觀隨意性。

　　第三節 債券及其評價

　　一、債券及其構成要素

　　債券，是債務人依照法定程序發行， 承諾按約定的利率和日期支付利息，并在特定日期償還本金的書面債務憑證。

　　一般而言，債券包括面值、期限、利率和價格等基本要素。

　　二、債券的評價

　　（一）債券的估價模型

　　債券的估價是對債券在某一時點的價值量的估算，是債券評價的一項重要內容。對于新發行的債券而言，估價模型的計算結果反映了債券的發行價格。

　　1.債券估價的基本模型

　　債券估價的基本模型，是指對典型債券所使用的估價模型，典型債券是票面利率固定，每年年末計算并支付當年利息、到期償還本金的債券。這種情況下，新發行債券的價值可采用如下模型進行評定：

　　

　　式中符號的含義與債券估價的基本模型相同。

　　（二）債券收益的來源及影響收益率的因素

　　債券的收益主要包括兩方面的內容：一是債券的利息收入；二是資本損益，即債券買入價與賣出價（在持有至到期的情況下為到期償還額）之間的差額，當賣出價高于買入價時為資本收益，反之為資本損失。此外，有的債券還可能因參與公司盈余分配，或者擁有轉股權而獲得額外收益。

　　決定債券收益率的因素主要有債券票面利率、期限、面值、持有時間、購買價格和出售價格。