第三單元 企業人力資源需求的總量預測①

　　【學習目標】
　　通過學習，掌握企業人力資源需求總量預測的各種基本概念和基本方法。
　　【知識要求】
　　影響企業人員需求的因素有很多，而且不同人員的影響因素各不相同，因此，在做人力資源需求預測時，必須根據崗位的特點分析其影響因素，確定合理而具體的影響參數
　　1．影響企業專門技能人員需求的參數有：企業戰略、組織結構、銷售收入(利潤)、產值產量、總資產(凈資產)、總成本、追加投資、人工成本、勞動生產率、出勤率、能源消耗情況、定額工時、作業率和廢品率等。
　　2．影響專業技術人員需求的參數有：企業戰略、組織結構、銷售收入(利潤)、產值產量、總資產(凈資產)、總成本、追加投資、人工成本、出勤率、生產技術水平、新項目投資、科研項目、科研經費、科研成果、研究成果獲獎，以及科技成果轉讓等。
　　3．影響經營管理人員需求的參數有：企業戰略、組織結構、銷售收入(利潤)、產值產量、總資產(凈資產)、總成本、追加投資、人工成本、勞動生產率、出勤率、能源消耗情況、企業管理幅度、企業信息化程度、信息傳送速度、決策速度，以及企業其他各類人員的數量等。
　　【能力要求】
　　本單元與下一單元將以A企業為例介紹各種人員需求預測方法的應用。需要指出的是，由于A企業要求對實際數據進行保密，本節中有關A企業的所有數據都經過不同程度的處理，并非原始數據，因此，數據實際參考價值弱，請讀者重點理解預測方法的運用。
　　一、A企業人員總量需求預測
　　(一)趨勢外推法
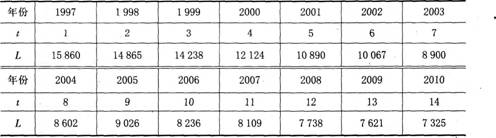
　　趨勢外推法是利用慣性的原理，對企業人力資源需求總量進行預測。根據調研結果，A企業人員總量的數據見表1—6，其中t表示年度，為自變量；L表示人員總數，為因變量。
　　表1—6企業員工總數時間序列統計表
　　
　　1．定性分析
　　(1)根據近些年來的企業人力資源管理所采取的減員增效策略，可以作出“短期內該企業的人數將持續降低，至少將保持持平的發展狀態”的推斷。
　　(2)實際上，企業人數不可能一直下降到0，因為在現實的生產條件下，企業要保證生產產品的銷售量，賺取利潤，還必須具備一定規模的員工人數，而不可能是“無人工廠”或采用“機器人”的生產模式。因此，做函數擬合的曲線不應具有一直向下的趨勢。
　　2．函數擬合
　　將上表輸入到SPSS，作函數擬合，本文選用九種函數對企業員工總數的趨勢做出擬合，見表1—7。
　　
　　上述公式中，L為人員總數，t為時間變量，bi為系數。通過SPSS分析，上述9種函數做擬合的結果見表1一7。
　　表1—7曲線擬合結果表
　　
　　續表
　　
　　3．模型篩選
　　根據表1一8所反映的信息，可以判斷，在時間序列曲線估計的9種模型中，所有模型的F值都大于10，其顯著度P都基本接近0，這說明用這些曲線做人數估計擬合是符合要求的，也就是說可以選用這些曲線做擬合。
　　表1—8各個模型的顯著性、判定系數及標準誤差值表

　　觀察表1—8第二列的數據，發現雙曲線與S曲線模型的R2比較小，而一般情況下，R2>0．8才認為有效，所以這兩種曲線應舍棄。另外，還能從表中發現復合函數、生長模型和指數函數這三個模型的預測結果是完全相同的，它們的判定系數、顯著性以及標準誤差值也是完全相同的，這就是說，這三個函數只取一個就可以了。因此保留對數函數、二次函數、三次函數、復合模型、冪指數模型。
　　(二)回歸分析法
　　回歸分析法是依據相關性原理對人力資源需求的總量進行預測。在項目進行中，通過對企業銷售收入、利潤、資產、產值、能源消耗量、設備數量的調查，取得了大量數據。在對這些數據進行必要的整理匯總和處理之后．繪制出散點圖，發現銷售收入、總資產、設備等方面的數據變化趨勢具有連續性和規律性，而利潤、產值、能源消耗量等數據，由于受企業辦社會、國家限產等企業外部環境條件的影響較大，使它們的變化趨勢不規則，從而導致這些指標的有效性明顯降低。因此，經過數據檢驗和相關分 析，選擇銷售收入、總資產、設備數量作為自變量，以企業員工總數為因變量，進行回歸分析。回歸分析檢驗結果，見表1—9。
　　表1—9回歸分析檢驗表
　　
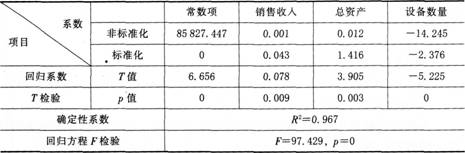
　　1．確定性系數R 2=0．967，趨于1，說明回歸方程擬合優度高。
　　2．回歸方程F檢驗的顯著度P為0，小于顯著性水平0．05，因此整個回歸方程線性關系顯著，可建立線性回歸模型。
　　3．回歸系數顯著性T檢驗中所有系數的P值均小于顯著性水平0．05，可見三個變量與被解釋變量月工資額的關系顯著，應保留在回歸方程中。根據表1—8，回歸方程表示如下：
　　L=85 827．447+0．001R+0．012A-14．245F
　　標準化方程為：L=0．043R+1．416A-2．376F
　　式中，L為企業員工總數；R為銷售收入；A為總資產；F為設備數重。
　　根據A企業“十二五”期間的戰略規劃資料，查得銷售收入、總資產和設備數量2011—2016年的規劃數據，將該數據代入回歸方程，即可得到2011—2016年企業人數的預測結果。

　　(三)運用灰色預測理論進行預測
　　選取表1一6中1997—2010年的企業人員總數統計數作為預測的基礎數據，見表1一10。
　　表1—10灰色系統預測基礎數據表
　　
　　應用灰色系統GM(1，1)模型，K=0，1，…，13，分別代表1997年、1998年、……、2010年，X(O)(K)為第K年企業員工總數。設X(1)(K+1)為累加到第K年的企業員工總數，即對X(O) (K)做一次累加生成。則：
　　
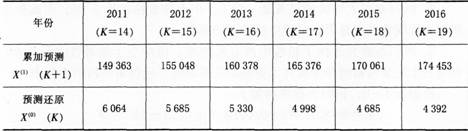
　　由此可以推導出未來年度企業員工總數的累加生成數，將累加預測做還原，即得到預測數值，見表1—11(K=13時，預測累計值為143 299)。
　　表1—11灰色系統預測值表
　　
　　(四)利用模型進行預測
　　在企業的發展戰略中，有關未來5年銷售收入、利潤、投資額(包括投入設備)等數據的計劃，則有未來銷售收入等各個計劃的數據，根據以上方程，代入這些自變量，得到以下預測結果見表1一12。
　　表1—12最終結果形成表人

　　本文認為各個模型的預測結果沒有重要與否的區別，即認為它們的權重相同，將這些模型的預測結果做平均，可以得到2011—2016年的企業員工總數最終預測結果。
　　可以看到。2011年上面7種模型預測結果平均值為7049人，實際上該企業2011年年底企業人數為7103人。這說明，預測值與實際值存在一定的誤差,需要連續觀察修正。要做長期預測，必須要做好隨時修正的準備，也就是報考預測：因為每個預測值都會被依次檢驗到，那么，當真實值出現時，需要不斷比較其與預測值之間的差距，并對后續的一系列預測結果做調整。由于2011年的真實值出現了，且預測誤差率為(7049—7 103)／7 103=-0．76％。這個數值是比較低的。用這個誤差率對2011—2016年人數預測值進行修正。即用每個預測值加上調整值，得到修正后的企業人員預測值，見表1一13。
　　表1—13企業201 1—2016年員工總數修正預測值

　　二、企業專門技能人員總量預測
　　(一)企業勞動定員定額分析
　　1．定性分析
　　由表1一14可見．專門技能人員在企業總人員中所占的比例基本保持在70％左右，而近年來隨著數控設備等新型設備的不斷引進，A企業有幾個裝備好的車間和分廠基本上實現了加工的自動控制或者局部自動化，這種趨勢還將不斷加強。設備的引進，隨之而來的是加工的精細化，加工質量和速度的提高以及對生產工人需求的逐步減少。從表1一14中不難發現，事實上近年來專門技能人員的比例的確是有所下降的，至2010年，專門技能人員所占的比例為67．19％，如果未來幾年繼續下降的話，有可能會達到65％的比例。因此，以人員比率法推算，按70％～65％的比例，可以大體判斷企業專門技能人員的總量范圍見表1—15。
　　表1—141997—2010年專門技能人員數量狀況表

　　續表

　　表1—15企業專門技能人員總量范圍判斷表

　　2．采用勞動效率定員法進行預測

　　通過調研,搜集到A企業甲、乙兩種系列產品各基本生產工人的勞動定額工時，歷年平均出勤率、平均作業率、歷年廢品率、企業歷年產品產量等一系列數據，以及企業2011一2016年主要產品產量的計劃指標和數據。預測某一工種崗位人員的需求人數，通常利用以下公式進行預測：
　　(1)定額完成率=實際完成定額工時總數／實作工時總數。
　　(2)實作工時總數=制度工時總數一缺勤工時總數一非生產工時總數一停工工時總數+加班加點工時總數，或者=制度工時總數×工時利用率+加班加點工時總數。
　　(3)工時利用率=作業率×出勤率。
　　(4)出勤率=出勤工時／制度工時。
　　(5)作業率=實作工時／出勤工時。
　　(6)需求人數=計劃定額工時總數×(1+廢品率)／(2 000×出勤率×作業率×定額完成率)。
　　最后一個公式是人員需求預測的最終公式，其中2 000是每年每個員工滿額的制度工作工時數。
　　在進行崗位人員需求預測時，根據采集到的統計數據，在作業率、出勤率、廢品率和定額完成率等指標已知的情況下，可以根據下列數據，對鉗工和數控機床操作工需求人數進行核算。
　　(1)已知鉗工2010年的甲產品單件定額工時為164．255小時，乙產品單件定額工時為271．377小時，2010年甲產品產量為1415臺，乙產品產量為1 054臺。2010年的平均作業率為90．2％，平均出勤率為98．6％，廢品率為0．09％，平均定額完成率為l28％，則2010年鉗工崗位人員需求人數為：
　　2010年鉗工崗位人員需求人數
　　=(164．255 × 1 415+271．377×1 054)×(1+0．09％)÷(2 000 × 98．6％× 90．2％× l28％)=227．917≈228(人)
　　但實際上，鉗工當年的人數為239人，這就是說，鉗工富余11人(239-228=11)。
　　(2)已知數控機床操作工2010年的甲產品單件定額工時為52．785小時。乙產品單件定額工時為87．21小時，2010年甲產品產量為1 415臺，乙產品為1 054臺。2010年平均作業率、平均出勤率、廢品率、平均定額完成率同上，則2010年數控機床操作工崗位人員的需求為：2010年數控機床操作丁：(52．785×1 415+87．21 × 1 054)(1+0．09％)／崗位人員需求量(2 000×128％×90．2％×98．6％)=73．243≈73(人)
　　2010年數控機床操作工的實際人數是68人，這說明數控機床操作工還欠缺5人(68+73=--5)，這個工種的工作有些吃緊，因此，工人在實際工作中需要加班加點才能完成生產任務。
　　依次可計算出所有實行工時定額管理工種的定員人數，并填入表1—16。
　　表1—16基本生產工人2010年定員人數表

　　一般來說，單件產品的定額工時總是呈下降趨勢的，產品剛上線時，單件產品定額工時通常比較高，但隨著產品產量的加大，設備操作的熟練以及工人技能的提高,單件產品定額工時就會隨之下降,這種下降趨勢不是無限的，到了某個點，就會保持穩定狀態，這時產品也就到了成熟期。進行單件產品工時定額的預測應以產品成熟期的數據為基礎。
　　A企業根據甲、乙產品的單件定額工時的預測數據，再結合“十二五”規劃里甲、乙產品產量的數據，就可以根據定員定額公式推斷專門技能人員基本生產工所需要的員工總數。計算結果見表1一17。
　　表1—17專門技能人員基本生產工人數預測表

　　(二)回歸分析
　　可以有兩種方式作多元回歸方程：一是利用企業產量產值等數據做自變量，以專門技能人員人數為因變量做回歸；二是以經營管理人員人數、專業技術人員人數、企業員工總數做自變量。以專門技能人員人數做因變量做回日。第一種方式的問題在于企業的各種指標到底是與員工總數相關，還是與專門技能人員人數相關。列入自變量的指標在未來六年中的規劃數據是否齊全：第二種方式的問題在于企業員工總數的值必須是經過預測后的調整值。而經營管理人員、專業技術人員在做回歸時采用的是真實值，如何知道其未來六年的預測值。
　　查閱調查數據．發現企業的很多指標都沒有未來規劃值，也就是說企業戰略沒有對這些具體指標作規劃，比如能源消耗、工資水平、勞動生產率水平等。而且專門技能人員在多元回歸上還存在大量數據空白，因此本例只能選擇一元回歸，用已知的數據來進行預測。
　　現在考慮以企業人員總數為自變量，專門技能人員人數為因變量，設計一元回歸線性方程。先利用SPSS做相關分析，得到企業人員總數與專門技能人員人數的相關系數為0．998，顯著度P值為0，可見兩者高度相關，這也符合前面的定性分析，即專門技能人員與企業員工總數基本保持在70％。說明可以利用企業人員總數來做預測，一元回歸方程的形式如下：
　　Y=α·X+b
　　式中，Y為專門技能人員的人數；X為企業人員總數；a為回歸系數；b為常數項。
　　將表1—14的數據輸入計算機。利用SPSS進行回歸分析，即可得到回歸方程：
　　Y=0．73X-297．531
　　將前面表1—12中預測的2011—2016年的企業員工總數帶人方程，可以得到專門技能人員在未來6年的預測值，見表1—18。
　　表1—182011—2016年專門技能人員人數預測值表

　　將表1—18中的數值與表1—15相對照．發現這些數據全部符合定性判斷的范圍，這說明一元回歸分析的結果是具有一定可靠性的。

　　三、企業專業技術人員總量預測
　　影響企業專業技術人員數量的因素很多，本例收集了1999—2010年A企業的專業技術人員數量、銷售收入、利潤、資產、產值、能源消耗量、設備數量等數據，經過初步處理發現：利潤、產值、能源消耗量因受國家政策和社會情況影響較大．不宜引入回歸方程：企業員工總數與專業技術人員數量線性關系不顯著，也不宜引入回歸方程；而銷售收入、科技支出、設備數量變化趨勢連續，跳動比較有規律，且與企業專業技術人員數量有明顯線性關系，可以引入回歸方程。因此，本例以企業的銷售收入、科技支出、設備數量為自變量，以專業技術人員數量為因變量，建立回歸預測模型，運用SPSS統計分析軟件進行分析處理，得出回歸方程：
　　y=866．729+0．070x 1-0．171x2-0．107x 3
　　式中，y為企業專業技術人員總數；x1為企業銷售收入；x2為科技支出；x3為設備數量。
　　將企業1999—2010年的銷售收入、科技支出和設備數量分別代入回歸方程，得到企業1999—2010年的專業技術人員的預測人數，與實際人數進行對比，見表1一19和圖1一20。
　　表1—19    1999—2010年企業專業技術人員實際值與預測值比較人

　　
　　由圖1—20中可以直觀看出，企業專業技術人員的預測值的變化趨勢基本反映了實際值的變化趨勢。由此可以判斷，我們所建立的回歸模型用來預測企業專業技術人員的偏差率比較低．可靠度較高。
　　根據A企業“十二五”規劃的要求．將2011—2016年該企業的銷售收入、科技支出、設備數量的數據代入回歸方程，得到2011一2016年該企業專業技術人員的預測值，匯總于表1—20。
　　表1—20 2011一2016年A企業專業技術人員人員人數預測值

　　四、企業經營管理人員總量預測
　　影響企業經營管理人員數量的因素很多，本例經過收集、處理、分析和篩選，選擇了員工總數、銷售收入、信息化投入作為自變量，以經營管理人員為因變量，建立回歸預測模型，運用SPSS統計分析軟件進行分析處理，
　　得到回歸方程：
　　Y=-77．912+0．199x1+0．023x2-33．699x3
　　式中，y為企業經營管理人員數量；x1為員工總數；x2為銷售收入；x3為信息化投入。
　　將企業1999—2010年的員工總數、銷售收入、信息化投入分別代入回歸方程，得到企業1999—2010年的經營管理人員的預測人數，與實際人數進行對比，見表1—21和圖1一21。
　　表1—211999—2010年企業經營管理人員實際值與預測值比較人

　　
　　由圖1—21中可以直觀看出，企業經營管理人員的預測值的變化趨勢基本反映了實際值的變化趨勢。由此可以判斷，我們所建立的回歸模型用來預測企業專業技術人員的偏差率比較低，可靠度較高。
　　根據A企業“十二五”規劃的要求．將，2011—2016年該企業的員工總數、銷售收入、信息化投入的數據代入回歸方程，得到2011—2016年該企業經營人員的預測值，匯總于表1一22。
　　表1—222011—2016年A企業經營管理人員人數預測值

　　教材分析：2014年企業人力資源管理師考試教材對比分析

　　報考信息：2014年11月人力資源管理師考試時間：11月23日｜報名時間

　　課程輔導：為方便廣大學員充分備考，233網校“2014年人力資源管理師HD高清課件”開始招生，輔導課程：VIP班，套餐班，精講班，預測班，應用技巧班。免費試聽>>