一、考題回顧

題目來源1月6日 下午 黑龍江省哈爾濱市 面試考題

試講題目1.題目：勾股定理

2.內(nèi)容：

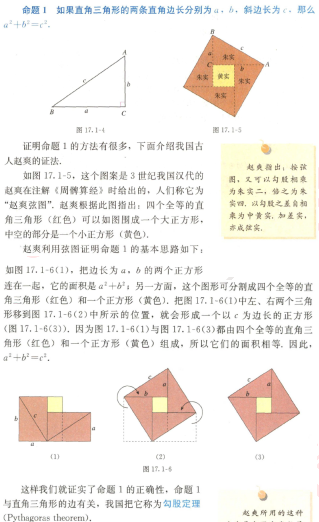
3.基本要求：

(1)要有板書;

(2)試講十分鐘左右;

(3)條理清晰，重點(diǎn)突出;

(4)學(xué)生掌握勾股定理的證明方法。

答辯題目1.勾股定理的教學(xué)過程中，體現(xiàn)了什么數(shù)學(xué)思想?

2.常見的三組勾股數(shù)是什么?

二、考題解析

【教學(xué)過程】

(一)引入新課

出示“國(guó)際數(shù)學(xué)家大會(huì)會(huì)徽”，提出問題：會(huì)徽?qǐng)D案有什么特別的含義嗎?蘊(yùn)含什么樣的數(shù)學(xué)奧秘?

(二)探索新知

活動(dòng)1：出示“畢達(dá)哥拉斯朋友家地板磚圖”。

引導(dǎo)學(xué)生發(fā)現(xiàn)理解圖形中全等的直角三角形的某種數(shù)量關(guān)系，并提出問題：等腰直角三角形三邊長(zhǎng)具有怎樣的關(guān)系?引導(dǎo)學(xué)生利用面積規(guī)律整理歸納得出：等腰直角三角形兩條直角邊的平方和等于斜邊的平方。

問題1：一般的直角三角形是否也具有類似規(guī)律?引導(dǎo)學(xué)生在網(wǎng)格圖利用面積探究規(guī)律并歸納出：直角三角形兩條直角邊的平方和等于斜邊的平方。

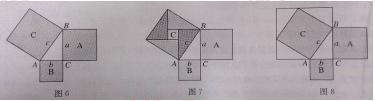
用a,b表示c的面積，如圖7用“割”的方法可得c²=1/2ab×4+(a-b)²;如圖8，用“補(bǔ)”的方法可得c²=(b+a)²-1/2ab×4，經(jīng)過整理都可以得到a²+b²=c²，即直角三角形兩直角邊的平方和等于斜邊的平方。

活動(dòng)2：引入趙爽弦圖，小組合作完成課本拼圖法證明勾股定理，并利用數(shù)學(xué)語(yǔ)言表達(dá)勾股定理：在Rt△ABC中，兩直角邊長(zhǎng)為a、b，斜邊長(zhǎng)為c，則a²+b²=c².

(三)課堂練習(xí)

練習(xí)1：設(shè)直角三角形的兩條直角邊分別為a和b，斜邊長(zhǎng)為c。

(1)已知a=6，c=10，求b。

(2)已知a=5，b=12，求c。

(3)已知c=25，b=15，求a。

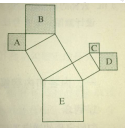
練習(xí)2:如圖,圖中所有三角形為直角三角形,四邊形都是正方形,已知正方形A,B，C，D邊長(zhǎng)分別是12,16,9,12,求最大正方形E的面積。

(四)小結(jié)作業(yè)

課堂小結(jié)：

提出問題:勾股定理的內(nèi)容是什么?它有什么作用?你本節(jié)課有哪些收獲?

【板書設(shè)計(jì)】略

引導(dǎo)回顧:勾股定理探究過程及內(nèi)容。

課后作業(yè)：

查找勾股定理的有關(guān)史料,趣間及其他證明方法。

下載233網(wǎng)校APP，可獲取教師資格證面試真題！

小編推薦：教師資格證面試考試流程 面試考生須知

真題推薦：歷年教師資格證面試真題>>>

通關(guān)秘籍：教師資格證面試如何快速通關(guān)？233網(wǎng)校講師將面試情景還原，助你一舉攻下“結(jié)構(gòu)化面試+試講+答辯”三大內(nèi)容，實(shí)戰(zhàn)通關(guān)！免費(fèi)體驗(yàn)>>