二、簡答題(本大題共5小題,每題7分,共35分)
9.
系,并求出反射光線的方程。若將反射光線繞平面鏡的法線旋轉一周,求所得的旋轉曲面的方程。
以此光線與平面的交點為原點,鏡面所在平面為xOy,平面建立空間直角坐標系,如下圖:
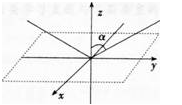
則入射光線所在直線過原點且在yOz坐標面上,所以入射光線的直線方程為z=ycota(y>0)。
而反射光線與入射光線關于z軸對稱,所以反射光線的直線方程為z=-ycota(y>0)。
而此時法線為z軸,故將反射光線繞平面鏡的法線旋轉一周,即是繞z軸旋轉一周。則得出旋轉曲面的方程是將反
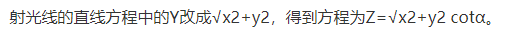
10.

11.某飛行表演大隊由甲、乙兩隊組成。甲隊中恰好有噴紅色與綠色噴霧的飛機各3架。乙隊中僅有3架噴紅色煙霧的飛機。在一次飛行表演中,需要從甲隊中任意選出3架飛機與乙隊飛機混合編隊進行表演,并任意確定一架飛機作為領飛飛機,求領飛飛機是噴綠色煙霧的概率。
分兩步進行計算,先選出含有噴綠色煙霧的飛機的概率再選領飛的飛機是噴綠色煙霧的概率,最后乘起來即得。

12.闡述確定數學課程內容的依據
在普通高中課程標準中規定:
必修課程內容確定的原則是:滿足未來公民的基本數學需求,為學生進一步的學習提供必要的數學準備。
選修課程內容確定的原則是:滿足學生的興趣和對未來發展的需求,為學生進一步學習、獲得較高數學素養奠定基礎。
在仔細研讀課程標準以及普通高中教材結合自身的教學經驗,我認為確定教學內容應依據數學課程標準、單元目標和具體數學知識點三者的結合。確定教學內容時,特別要注意以下三點:
一是數學知識的主要特征。一個數學知識點內容是極為龐雜的,我們應該選擇該數學知識點最本質的東西作為教學的重點。
二是學生的需要。確定知識點的教學內容也不是由教材一個要素決定的,還涉及學生認知發展階段性的問題。因此也不可能是教材有什么我們就教什么、學什么,我們只能選擇教材內容與學生認知發展相一致的內容作為教學內容。
三是編者的意圖。編者的意圖主要是通過例題以及課后的練習題來體現的。數學例題以及課后練習題的重要性在數學課程中要遠遠高于其他學科.因為數學例題以及練習題是數學課程內容建設一個不可或缺的組成部分。在其他課程中,練習題最多只是課程內容的重現,有的只屬于教學領域,作為一種教學手段,對課程本身并沒有很大影響。但數學課不是這樣,數學課“教什么”在相當程度上是由練習題或明或暗指示給教師的。
13.舉例說明向量內容的學習對高中生理解數學運算的作用。
平面向量是高中數學引入的一個新概念。利用平面向量的定義、定理、性質及有關公式,可以簡化解題過程,便于學生的理解和掌握。
向量運算可以提高學生針對數學運算的理解層次,學生從最初接觸運算都是數與數之間的運算,而加入向量運算之后,向量運算涉及的數學元素更高,比如說實數、字母、甚至向量,甚至還可以把幾何圖形加入運算當中,這本身是對數學層次更大的一個提高。而且向量運算對數學的思想也體現得比較多,比如在解析幾何當中,或者是在平面幾何當中,向量應用確實很方便,一個運算既有代數意義又有幾何意義,但是到了立體幾何時,我覺得向量運算僅僅就變成算術了,算術對立體幾何本意是沒有一點想象的,就是它到底讓學生重點掌握什么,掌握運算還是掌握思維和想象。
一、向量在代數中的應用。根據復數的幾何意義,在復平面上可以用向量來表示復數。這樣復數的加減法,就可以看成是向量的加減.復數的乘除法可以用向量的旋轉和數乘向量得到,學了向量,復數事實上已沒有太多的實質性內容。因而選學內容也就不難理解了。另外向量所建立的數形對應也可用來證明代數中的一些恒等式、不等式問題,只要建立一定的數學模型,可以較靈活地給出證題方法。
二、向量在三角中的應用。當我們利用單位圓來研究三角函數的幾何意義時,表示三角函數就是平面向量。
利用向量的有關知識可以導出部分誘導公式。由于用向量解決問題時常常是從三角形人手的,這使它在三角里解決有關三角形的問題發揮了重要作用,一個最有力的證據就是教材中所提供的余弦定理的證明:只要在根據向量三角形得出的關系式的兩邊平方就可利用向量的運算性質得出要證的結論.它比用綜合法提供的證明要簡便得多。
三、向量在平面解析幾何中的應用。由于向量作為一種有向線段,本身就是有向直線上的一段,且向量的坐標可以用起點、終點的坐標來表示,使向量與平面解析幾何特別是其中有關直線的部分保持著一種天然的聯系。平面直角坐標系內兩點間的距離公式,也就是平面內相應的向量的長度公式:分一條線段成定比的分點坐標,可根據相應的兩個向量的坐標直接求得;用直線的方向向量(a,b)表示直線方向比直線的斜率更具有一般性,且斜率實際是方向向量在a=0時的特殊情形。另外向量的平移也可用來化簡二次曲線,即通過移動圖形的變換來達到化簡二次曲線的目的,實際上與解析幾何中移軸變換達到同樣的效果。
四、向量在幾何中的應用。在解決幾何中的有關度量、角度、平行、垂直等問題時用向量解決也很方便。特別是平面向量可以推廣到空間用來解決立體幾何問題。例如在空間直線和平面這部分內容中,解決平行、相交、包含以及計算夾角、距離等問題用傳統的方法往往較為繁瑣,但只要引入向量,利用向量的線性運算及向量的數量積和向量積以后,一切都歸結為數字式符號運算。這些運算都有法則可循,比傳統的方法要容易得多。
總之,平面向量已經滲透到中學數學的許多方面,向量法代替傳統教學方法已成為現代數學發展的必然趨勢。向量法是一種值得學生花費時間、精力去掌握的一種新方法,學好向量知識有助于理解和掌握與之有關聯的學科。
因此在中學數學教學中加強向量這一章的教學,可以更好地為學習其他知識做必要的準備。但傳統教學思想對向量抵觸較大,許多教師認為向量法削弱了學生的空間想象能力,且學生初學向量時接受較為困難,這就要求我們不斷探索,找出最佳的教和學的方法,發揮向量的作用,使向量真正地成為現代數學的基礎。



