六、教學設計題(本大題1小題，30分)
17.“基本不等式”是高中數學教學中的重要內容，請完成下列任務：
(1)在“基本不等式”起始課的“教學重點”設計中，有兩種方案：
①強調基本不等式在求數值中的應用，將基本不等式的應用作為重點。
②強調基本不等式的背景，過程與意義，將學生感受和體驗“基本不等式”中“基本”的意義作為教學重點。
你贊同哪種方案?簡述理由。(10分)
(2)
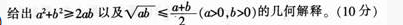
(3)為了讓高中生充分認識“基本不等式”中“基本”的意義，作為教師應該對此有多個維度的理解，請至少從兩個維度談談你對“基本”意義的認識。(10分)
(1)我更贊同第二種方案，理由如下：
①本節課定位為“基本不等式”的起始課，它是在學生已經系統地學習了不等式關系和不等式性質，掌握了不等式性質的基礎上進行教學的。學生對于“基本不等式”還處于初步感知階段，不能一步就理解如何實現基本不等式在求解簡單最大(小)值當中的應用，因此，在“基本不等式”的起始課當中，應當先讓學生結合基本不等式的背景和意義進行自主探索，了解不等式的證明過程，加深印象及存在原因后再學習應用會更好。
因此，從這三點來看，基本不等式的起始課的教學重點應該采用第二種方案,即強調基本不等式的背景、過程及意義，將學生感受和體驗“基本不等式”中“基本”的意義作為教學重點。
(2)a2+ b2≥2ab的幾何解釋是:大正方形的面積大于四個三角形的面積和,當且僅當a=b時，等號成立(即正方形的對角線將正方形分成4個等腰直角三角形，正方形的面積等于四個等腰三角形的面積和)。(如圖所示)
認識”基本”二字,是學習基本不等式這一節內容的前提，事實上,該不等式反映了實數的兩種基本運算(即加法和乘法)所引出的大小變化，這一本質不僅反映在其代數結構上,而且也有幾何意義，由此而生發出的問題在訓練學生的代數推理能力和幾何直觀能力上都發揮了良好的作用。因此,必須從基本不等式的代數結構和幾何意義兩方面人手,才能讓學生深刻理解它的本質。
