相信我,做人力資源的都很討厭計算題的,畢竟人力資源伙伴們大部分都是文科生,對計算天生苦手。然而,計算題在技能卷占得比分卻不少啊,匈牙利法是很多小伙伴們沒弄明白的一個難點,小編也是翻閱了無數資料,請教了很多高手,徹底弄明白以后,以最簡單易懂的方法跟大家分享這個知識難點,答應我,看完這篇文章以后,不要再討厭它好嗎?
一、什么是匈牙利法?
是一種在多項式時間內求解任務分配問題的組合優化算法,通俗點講,就是實現人員與工作任務配置合理化、科學化的典型方法(教材P115)
二、匈牙利法的應用
匈牙利法是一個很復雜的計算方法,運用到其他領域的算法非常復雜,但是用于人力資源領域你只需要了解如何解決公司工作任務合理分配的問題,比如公司有N個工作崗位空缺,每個崗位空缺需要有一定資格的人來填補。現在有M個人申請這N個工作。由于每個人工作能力不同,所以不同的人能勝任不同的工作。 現在己知每個人所能勝任的若干工作,求這M個人最多可以填補幾個工作崗位。 每個人只能做一份工作,每個工作崗位也只需要一個人,怎樣安排才能使效率最大化。
運用匈牙利法,解決員工任務合理指派問題時,應該具備兩個約束條件:員工數目與任務數目相等;求解的是最小化問題,如工作時間最小化、費用最小化等。(教材P115)
三、匈牙利法的計算
應用例題:單位有甲、乙、丙、丁、戊五名員工,需要在一定的生產技術組織條件下,完成A、B、C、D、E五項任務,各員工完成每項工作所需要耗費的工作時間見下表,求解:員工與任務之間如何配置,才能保證完成工作任務的時間最短?
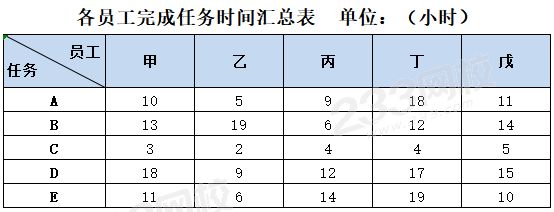
1、利用上表構造矩陣一,把數據提取出來。

2、對提取數據的矩陣一進行橫向的行約減,每一行數據減去本行數據中的最小數,得出矩陣二。

3、檢查矩陣二,如果矩陣二各行各列均有“0”,則跳過此步,否則進行縱向列約減,即每一列數據減去本列數據中的最小數,經變換得矩陣三。
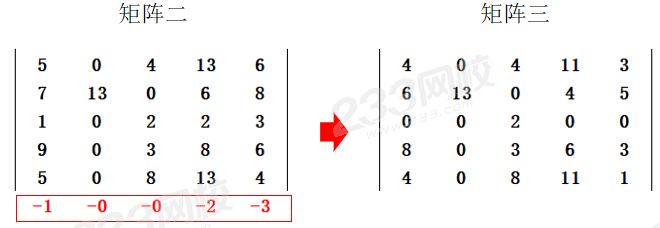
4、畫蓋0線,畫最少的線將矩陣三中的0全部覆蓋住,得到矩陣四,技巧:從含0最多的行或列開始畫蓋0線。
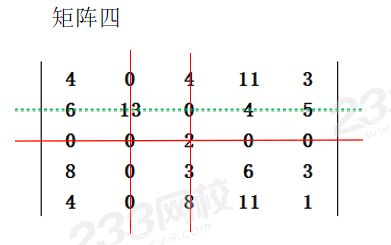
5、數據轉換,如果蓋0線的數目等于矩陣的維數 (即為行數或列數)則直接跳到第七步,若蓋0線的數目小于矩陣的維數則進行數據轉換,本例屬于后一種情況,應進行轉換,操作步驟如下:
(1)找出未被蓋0線覆蓋的數中的最小值λ,例中的λ=1;
(2)將未被蓋0線覆蓋住的數減去λ;
(3)將蓋0線交叉點的數加上λ。


6、重復第4步和第5步,直到蓋0線的數目等于矩陣的維數,本例最終矩陣見矩陣六。
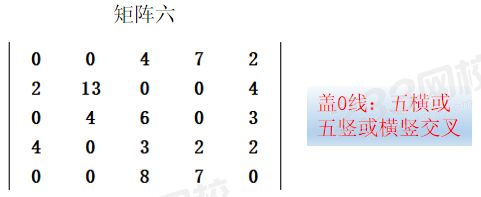
7、求最憂解。對N維矩陣找出不同行、不同列的N個0,每個0的位置代表一對配置關系,具體步驟:
(1)先找只含有一個0的行或列,將該行或列中的0打√;
(2)將帶√的0所在列或行中的0打×;
(3)重復以上(1)和(2)至結束,如果所有行列均含有多個0,則從0數目最少的行或列中任選一個0打√。

結果如矩陣七所示,員工甲負責任務A,員工乙負責任務D,員工丙負責任務B,員工丁負責任務C,員工戊負責任務E,得出員工配置最終結果:
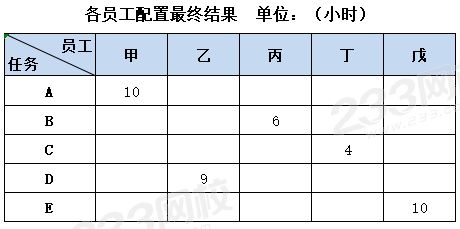
以上的講述,是不是比教材上面通俗易懂多啦?關鍵算法部分,用紅色標記好了,已經是用最簡單的方式給大家分解出來了,跟著步驟一步一步來,完全沒問題啦!今天的分享先到這里,以上是員工數量和任務相同時的案例,下期接著分享員工數量與任務數量不一致的匈牙利分配法,趕快收藏起來噢!



